142857×1=142857
142857×2=285714
142857×3=428571
142857×4=571428
142857×5=714285
142857×6=857142
142857×7=999999
ダイヤル数(ダイヤルすう)とは、乗法したときにその数の順序が崩れずに循環する数のことである。
http://ja.wikipedia.org/wiki/%ダイヤル数
221:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:37:54.05 ID:vAo4n4gE0
>>6
巡回符号みたいで面白いね
8:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:14:50.51 ID:iLUfBMmF0
1/3 = 0.333333333・・・
1/3 × 3 = ?
27:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:24:24.72 ID:NzNb0fHM0
>>8
電卓を使ってそれが出てくると本当に苛立つ時があった
19:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:19:49.60 ID:DSCO+UTu0
順極限(帰納極限、直極限)
逆極限(射影極限)
余極限
上極限
下極限
左極限
右極限
極限
23:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:21:57.05 ID:CPFasgB30
ほとんど整数
整数ではないが、整数に非常に近いことを意味する。どれほど近ければ十分であるのか明確な決まりはないが、一見して整数に近いとは分からないのに、近似値を計算すると驚くほど整数に近い数で、小数点以下の部分が「.000…」または「.999…」のように、0か9が数個連続する場合、このように表現される。
http://ja.wikipedia.org/wiki/ほとんど整数
26:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:23:17.14 ID:52G5mXY/0
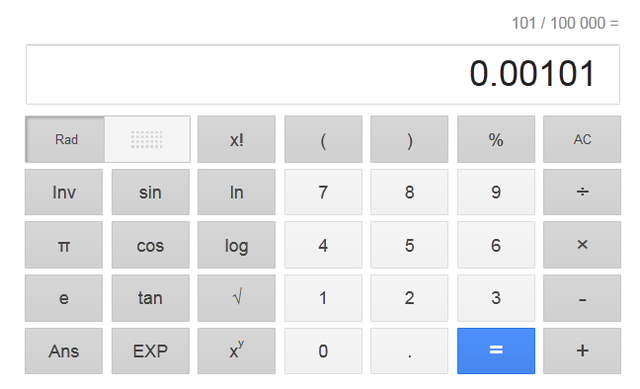
円周率に0がなんで出てくるのか分からん
割り算なら0出てきたら割り切れてるって事なんじゃないの
誰かおせーて
57:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:40:24.16 ID:azFli+NJ0
>>26
101/100000とかといっしよ
35:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:30:08.55 ID:L0Esf6h30
代数的5次方程式の解の公式と楕円関数の関係
39:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:32:03.94 ID:Y3KPFH9h0
>>35
ぜ、全然意味わからないぞ…………
48:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:36:23.11 ID:6dqkOZvL0
>>39
355/113 がよい近似値になるのは有名な話題で
wikipedia の 113 の項目でも紹介されている
113355 を分けて云々は覚えるための便法
某文庫本に書いてあった
36:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:31:10.85 ID:6dqkOZvL0
1 1 3 3 5 5
を前3つと後ろ3つに分けて分数
355/113
を作ると円周率πのよい近似値が得られる
53:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:38:32.89 ID:L0Esf6h30
最大値の原理
特定の楕円型および放物型の偏微分方程式の解が持つある性質のことを言う。大雑把に言うと、ある領域内でのある関数の最大値は、その領域の境界上に存在する、ということがこの原理では述べられている。特に、ある関数が領域の内部で最大値を取るのなら、その関数は一様に定数である、ということについて述べた原理は「強最大値原理」と呼ばれる。関数の最大値は領域の境界上で取られるが、領域の内部でも同様に起こり得る、ということについて述べた原理は「弱最大値原理」と呼ばれる。他に、ある関数をその最大に関して単純に境界で制限するような、さらに弱い最大値原理も存在する。
http://ja.wikipedia.org/wiki/最大値原理
コラッツ予想
コラッツの予想
http://www.tamagaki.com/math/CollatzProblem.html
64:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:46:16.44 ID:pQBDrIicO
ポアンカレ予想を解決したペレルマンはニートでおかんと二人暮らし
収入源はおかんの年金だった
71:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:48:38.56 ID:Y3KPFH9h0
>>64
そういう話も良いねw
78:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 01:52:58.14 ID:TF00TqUgO
円周率が完全ランダムの無限数列だとすれば、
理論上あらゆる数字の並びのパターンが含まれていることになる。
例えば45450721や191969といった並びになってる部分も必ずどこかにある。
理屈の上では桁がどんなに増えても成り立つ。

88:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:03:45.27 ID:DlPc0zuh0
1/9801
103:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:11:51.06 ID:DlPc0zuh0
1/9801に興味なさすぎワロタ
やっぱ面白いところを示さないとダメか
1/9801=0.
00 01 02 03 04 05 06 07 08 09
10 11 12 13 14 15 16 17 18 19
20 21 22 23 ...
90 91 92 93 94 95 96 97 99
で循環
104:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:13:23.51 ID:Y3KPFH9h0
>>103
すげぇ
105:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:13:51.70 ID:L0Esf6h30
コンパクト群はコンパクトリー群の射影極限
113:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:16:33.90 ID:DSCO+UTu0
>>105
イ`ヘ
/: :| ヽ
/ : :/ ヽ ___ _,,,:. .-: :´彡フ
_ノ\_∠: : : : : : : : :`: :-: :,:_:/彡 /
( : : : : : : : : : : : : : : `ゝ /
マ r::/: /: : | : : : : : : : : ::\ /
//: /: : : |: : | |: : |: _: : : :ヽ
ジ {/ 7|`\/i: /|:|/|´: : : : :|ヽ
〉 ,‐-‐、`|7 || |_::|,_|: : :|:::|: |
で / r:oヽ` /.:oヽヽ: :|: | :|
{ {o:::::::} {:::::0 }/: :|N
っ | ヾ:::ソ ヾ:::ソ /|: : |
!? ヽ::::ー-.. /ヽ ..ー-::: ヽ::| r--ッ
-tヽ/´|`::::::::::;/ `、 ::::::::::: /: i } >
::∧: : :|: |J \ / /::i: | /_ゝ
. \ヾ: |::|` - ,, ___`-´_ ,, - ´|: : :|:::|
ヽ: |::|\  ̄/ /| |: : :|: |
116:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:17:33.78 ID:L0Esf6h30
>>113
らしいよ
証明は読んだことないけど
110:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:15:23.87 ID:6dqkOZvL0
1/89 とか
112:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:16:32.50 ID:a6ASbAs30
>>110
詳しく
128:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:23:02.51 ID:6dqkOZvL0
>>112
フィボナッチ数を桁をずらして次々と足していったら 1/89 になる
http://ja.wikipedia.org/wiki/フィボナッチ数
125:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:22:10.31 ID:jm2gg8XP0
1、好きな一桁の数字を二つ並べる
2、二つの数字の和、の一の位を右に書いていく作業を続ける
3、15番目の数字は必ず0となる
例:
3,3,6,9,5,4,9,3,2,5,7,2,9,1,0
126:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:22:29.18 ID:DlPc0zuh0
誰でも親しみやすいのはコラッツ予想
ある自然数nに対して、以下の操作を有限回行なったとき、どのような自然数nでも必ず1になる
・nが奇数なら3倍して1加える(n←3n+1)
・nが偶数なら2で割る(n←n/2)
136:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:28:50.64 ID:Y3KPFH9h0
ガチの数学者とか意外と見てたりするのかね
146:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:34:01.78 ID:tKppQDQD0
>>136
大沢教授とか数学板かきこんでたよ
150:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:34:57.95 ID:Y3KPFH9h0
>>146
わりと見てるものなんだねwww
156:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:38:30.36 ID:tKppQDQD0
>>150
ちなみに大沢教授の講義では数学板のスレが講義printとして配られました
159:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 02:40:18.03 ID:Y3KPFH9h0
>>156
面白い教授だね。実りあるレスも少なくないし良いアイディアだ。
180:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:03:25.92 ID:s5c13KgV0
歴史上の数学者でこいつが多分一番すごいってのは誰?
やっぱガウス?
ドイツの数学者、天文学者、物理学者である。彼の研究は広範囲におよんでおり、特に近代数学のほとんどの分野に影響を与えたと考えられている。数学や磁気学の各分野には彼の名が付いた法則、手法等が数多く存在する。18-19世紀最大の数学者の1人である。
http://ja.wikipedia.org/wiki/ガウス
184:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:04:33.35 ID:Y3KPFH9h0
>>180
ラマヌジャンとか?

インドの数学者。極めて直感的、天才的な閃きにより「インドの魔術師」の異名を取った。
http://ja.wikipedia.org/wiki/シュリニヴァーサ・ラマヌジャン
188:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:09:32.37 ID:NubrBlxN0
>>180
決闘して死んだガロアさん

http://ja.wikipedia.org/wiki/エヴァリスト・ガロア
193:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:11:20.55 ID:El/68c4W0
確率0パーセントでも起こらないとは言えない
らしい
よく話題になる確率の問題を集めてみる
http://blog.livedoor.jp/nwknews/archives/4126636.html
202:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:20:18.19 ID:Ilv3R4t90
>>193
ルベーグ積分使うとよく出てくるよね
xy平面上の有理点の集合の面積(測度)は0とか
感覚的には何かがあるはずなのに0になっちゃう
203:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:23:10.12 ID:cJBMzykU0
数学科だけど
確率が連続分布のときに、幅をとらない一つの点では確率は0ってのがいまだになっとくいかない
229:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:42:15.97 ID:BO9td9js0
コンパスと定規があれば理論上、正17角形とか作図できるけど
実際に描いてみると誤差のせいで10回中9回くらいは15角形とかになる
230:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:42:44.18 ID:K+1Kf2sz0
クラスに同じ誕生日の人がいる確率は高めってのがいまいちわかんない(^q^)
247:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:53:32.67 ID:jmwklKNU0
>>230
wikipediaに分かりやすく書かれてる気がするけど
http://ja.wikipedia.org/wiki/誕生日のパラドックス
253:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 03:58:18.55 ID:jm2gg8XP0
マクローリン展開の美しさに涙を流してそこで勉強止まってる俺には早すぎるスレだな
255:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 04:00:32.13 ID:Y3KPFH9h0
>>253
e^(πi)=cosx+i*sinxがテイラーで示せた時に指数関数を三角関数で表せるヤバい公式があるのかと驚いたよ
257:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 04:10:52.44 ID:Ilv3R4t90
ラムゼー理論
エルデッシュが開拓した数学の組み合わせ論の一分野に、
ラムゼー理論という、哲学的な興味をそそるものがある。
ラムゼー理論の裏にある考え方は、完全な無秩序はあり得ないというものである。
無秩序の現れ方はスケールの大きさに関係する。どんな数学的条件でも、
十分大きな集合を探せばなんらかの秩序が見いだせるというものである。
たとえば、ほぼ同一直線上に見える8つの星を必ず含む、
星の最小集合を求めることなんかがそうである。
もっと簡単な問題だと、同性の2人の人を必ず含むという
人の集まりの最小人数や如何?答えは3人である。
このラムゼー問題は単純なものにみえるものでも、ひどく難解なものがある。
古典的なラムゼー問題に、パーティー会場で、少なくとも3人の招待客が互いに知り合いか、
または3人ともお互いに全く知らない招待客同士であるという状況が生まれるためには、最低何人の客を招かねばならないか、というものがある。答えは6人である。
3人を4人にすると、18人が必要かつ十分であることを
エルデッシュやグラハムなどが証明している。
5人にすると、答えは43人から49人の間のどれかの人数であることしか知られていない。
6人とすると、答えは102人から165人の間ということまで絞られているが、
何人と特定はできていない。
259:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 04:13:39.13 ID:jm2gg8XP0
クラス内で席替えをした時、前と同じ席に座ってる人数の平均は1
クラスが何人であろうと平均一人
1:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 18:22:08.55 ID:Y3KPFH9h0
昨晩立てたのが面白かったのでここでもぜひお話をお聞かせ願いたいです。
7:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 18:27:19.45 ID:p1M4PH7T0
0.999……=1
12:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 18:29:32.23 ID:Y3KPFH9h0
>>7
よくみるやつだねw
14:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 18:32:39.75 ID:GE2Ut43D0
>>12
2nと s
2mと t
nは偶数、mは奇数 s、tはそれぞれ正と負の数とすれば、一対一対応が成り立つ
だいたいこんな感じ
一般化して一対一対応が成り立つのがミソ
15:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 18:38:30.40 ID:Y3KPFH9h0
>>14
なるほど。1対1対応させるのに有限集合ではないことを考えればいいんですね(合ってますか?)
28:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:10:02.53 ID:GE2Ut43D0
>>15
あってる
29:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:12:25.79 ID:Y3KPFH9h0
8*1+1=9
8*12+2=98
8*123+3=987
8*1234+4=9876
8*12345+5=98765
8*123456+6=987654
8*1234567+7=9876543
8*12345678+8=98765432
8*123456789+9=987654321
これすごい
37:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:16:50.41 ID:eeP+gYCc0
31←素数
331←素数
3331←素数
33331←素数
333331←素数
3333331←素数
33333331←素数
333333331←素数じゃない
47:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:31:47.36 ID:1GcPyFKm0
長さ1の線分を1回転させられる領域の面積の最小値は0
50:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:36:34.71 ID:Y3KPFH9h0
>>47
それってA(0,0,0),B(1,0,0)とした線分ABについて考えるときx軸のまわりに回転させるってことかい?
51:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:40:17.13 ID:1GcPyFKm0
>>50
そうじゃなくてxy平面上に長さ1の線分があればそれをxy平面上において360°ぐるっと回転させる
52:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:41:45.18 ID:Y3KPFH9h0
>>51
それで面積0ってどうやるんだ…
53:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:46:27.94 ID:1GcPyFKm0
>>52
これは掛谷問題って問題でペロンの木が有名
54:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 19:50:31.30 ID:Y3KPFH9h0
>>53
調べてみてる。こんなの思いつかねえよ・・・
64:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 20:04:18.81 ID:Tb6HU2xY0
完全な球体があると仮定してそれを平面上に置くとどうなんの
浮くの?
68:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 20:06:52.48 ID:DlPc0zuh0
>>64
接地面積が0
触れてはいるんだけど浮きはしないんじゃない
1つ次元を落として、y=(x-1)^2のグラフがx軸と触れる長さは0だけど、触れていないわけではない
72:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 20:07:46.33 ID:GE2Ut43D0
>>64
数学的には接触面の面積0だけど、現実だとどうあがいても完全な球体は作られない
84:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 20:36:26.42 ID:MAhLvwal0
ガウスは、自分が発見した正17角形の作図法に感激し、
「私が死んだら、墓にこの図を彫ってくれ!」
と頼んだが、複雑過ぎたので彫ってもらえなかった。
87:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 20:42:01.84 ID:DlPc0zuh0
>>84
ワロタ
正5角形の作図
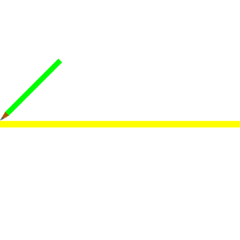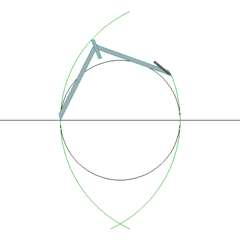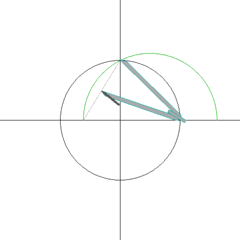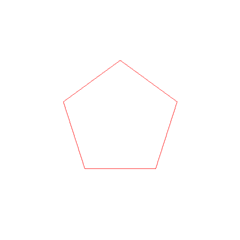
正17角形の作図
http://ja.wikipedia.org/wiki/:Regular_Heptadecagon_Inscribed_in_a_Circle.gif
http://ja.wikipedia.org/wiki/十七角形
最早きちがい
90:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 20:49:14.38 ID:Vw04DxZY0
>>87
すげぇwwwwwwww
102:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 21:13:39.90 ID:MAhLvwal0
サイコロを6回振ったとき、
1が連続で6回出る確率と、
1,2,3,4,5,6と順番に出る確率は等しい。
↑
ちょっと数学に詳しい人間にとっては当たり前だけど、
そうじゃない人間にとっては意外らしい。
119:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 21:43:09.90 ID:MAhLvwal0
デカルトには、午前中を寝て過ごす習慣があった。
そして、スウェーデン女王に朝五時から数学を教えるようになった結果、
半年で肺炎にかかり死亡した。
158:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 22:57:35.44 ID:91jQwjm40
5と6は相性が良い
x^2-6x+5=0
x^2-5x+6=0
x^2-5x-6=0
x^2-55x+666=0
x^2-665x+66666=0
はすべて整数解
159:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 23:02:02.96 ID:QglslyGS0
高校の時教科書に載ってた話だけど
赤道上で地球の裏側と同じ温度の場所が必ず一組以上ある
160:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 23:09:08.57 ID:MAhLvwal0
>>159
証明が知りたい
162:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 23:11:48.34 ID:EBmYREbl0
>>160
予想だけど、地球を太陽に射影したときの端点が同じになるということだと思う
163:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 23:12:54.00 ID:1GcPyFKm0
赤道上で直径となる2点A,Bと選ぶ
Aから経度θ進んだ点をP,その裏側をQとする
Pの温度をp(θ),Qの温度をq(θ)とする
f(θ)=p(θ)-q(θ)と定める
θ=0°のときP=A,Q=B
θ=180°のときP=B,Q=A
PとQが入れ替わっているのでf(0°)=-f(180°)
f(0°)=0とするとp(0°)=q(0°)となる
f(0°)≠0のときはf(0°)とf(180°)は異符号なので
f(θ)=0を満たすθが0°<θ<180°の範囲に少なくとも一つ存在する
このときp(θ)=q(θ)となる
165:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 23:14:54.33 ID:91jQwjm40
>>160
便宜上、赤道を東経0°から360°とする。
f(x)を(東経x°の温度)-(そのちょうど裏側の温度)
とする。
f(0)=0であれば、東経0°の点が条件を満たす。
f(0)>0であれば、f(180)=-f(0)<0より
中間値の定理から
0<t<180でf(t)=0となるtが存在する。
つまり裏側と同じ点が存在する。
f(0)<0も同様。
167:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 23:17:23.89 ID:MAhLvwal0
>>163>>165
理解したthx
140:以下、名無しにかわりましてVIPがお送りします:2013/03/17(日) 22:13:32.48 ID:A4d29Tqa0
数学者って本物の天才だよな